First Published 1 Jan 2024




This article provides code to calculate the linear distance across the Earth's surface between any two locations based on their geo-coordinates.

This will of course not be the same as the actual distance between the points if you travel between them by land/sea or air.
It also does not take into account differences in altitudes en route or at each location.

The code uses the Earth's average radius as the Earth is not an exact sphere - it is slightly flattened at the poles.

NOTE:
The distance from the Equator to the North Pole is approximately 10,000 kilometres.
This is because the metre was originally defined in 1790 as one ten-millionth of the distance from the North Pole to the Equator (Earth quadrant), measured along the Paris meridian. Later calculations showed the original calculations were not quite correct and the definition has been updated several times. Since 1983, the unit of length has been defined in terms of the distance travelled in one second by light in a vacuum where the time interval is based on the frequency of the Caesium atom

For more information, see History of the metre



Download

The example app supplied includes all code and allows you to calculate distances by entering latitude and longitude values.
You can also calculate the distances between pairs of UK postcodes




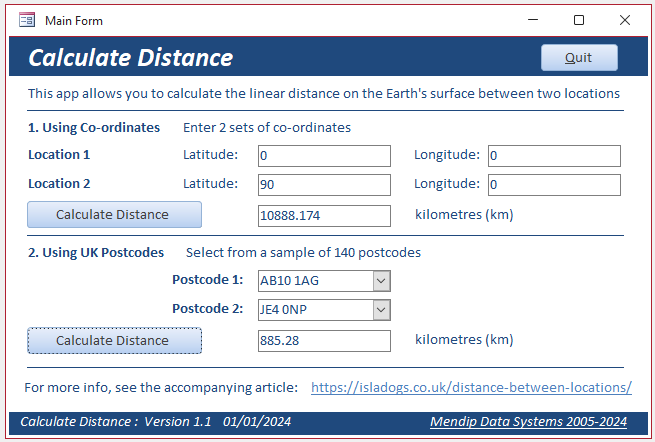
Click to download:           Calculate Distance      ACCDB file    (approx 0.6 MB zipped)



CODE:

Function GetDistanceKilometres(lat1Degrees As Single, lon1Degrees As Single, lat2Degrees As Single, lon2Degrees As Single)

Dim EarthSphereRadiusKilometres As Double
' Dim kilometerConversionToMilesFactor As Double
Dim lat1Radians As Single
Dim lon1Radians As Single
Dim lat2Radians As Single
Dim lon2Radians As Single
Dim AsinBase As Single
Dim DerivedAsin As Single
Dim Pi As Double

Pi = 3.14159265359

'Mean radius of the earth (replace with 3443.89849 to get nautical miles)
EarthSphereRadiusKilometres = 6371.001
'Earth radius at sea level is 6378. 137 km (3963. 191 mi) at the equator.
'It is 6356. 752 km (3949. 903 mi) at the poles
'Average value is 6371. 001 km (3958. 756 mi)

'OPTIONAL - Convert kilometers into miles
' kilometerConversionToMilesFactor = 0.621371

'Convert each decimal degree to radians
lat1Radians = (lat1Degrees / 180) * Pi
lon1Radians = (lon1Degrees / 180) * Pi
lat2Radians = (lat2Degrees / 180) * Pi
lon2Radians = (lon2Degrees / 180) * Pi

AsinBase = Sin(Sqr(Sin((lat1Radians - lat2Radians) / 2) ^ 2 + Cos(lat1Radians) * Cos(lat2Radians) * Sin((lon1Radians - lon2Radians) / 2) ^ 2))
DerivedAsin = (AsinBase / Sqr(-AsinBase * AsinBase + 1))

'Get distance from [lat1,lon1] to [lat2,lon2]
GetDistanceKilometres = Round(2 * DerivedAsin * EarthSphereRadiusKilometres, 3)
'Miles: = Round(2 * DerivedAsin * (earthSphereRadiusKilometers * kilometerConversionToMilesFactor), 2)

'Debug.Print GetDistanceMetres

End Function

Example Results (from the Immediate window):

' North Pole to South Pole
?GetDistanceKilometres(90,0,-90,0)
19844.489

' London to Auckland
?GetDistanceKilometres(52.5,0,-36.848461, 174.763336)
19422.035

' Paris to Rome
?GetDistanceKilometres(48.85341,2.3488,41.8999964, 12.4833314)
1106.126
' Actual road distance = approx 1420 km

'New York to San Francisco
?GetDistanceKilometres(40.730610, -73.935242, 37.773972, -122.431297)
4206.897

The second code sample allows you to calculate the distance between selected UK postcodes whose co-ordinates are stored in the supplied Postcodes table.



CODE:

Function TestDistanceKilometres(Postcode1 As String, Postcode2 As String) As Single

Dim lat1 As Single
Dim lon1 As Single
Dim lat2 As Single
Dim lon2 As Single

' Get co-ordinates for each postcodes from Postcodes table
lat1 = DLookup("Latitude", "Postcodes", "Postcode = '" & Postcode1 & "'")
lon1 = DLookup("Longitude", "Postcodes", "Postcode = '" & Postcode1 & "'")
lat2 = DLookup("Latitude", "Postcodes", "Postcode = '" & Postcode2 & "'")
lon2 = DLookup("Longitude", "Postcodes", "Postcode = '" & Postcode2 & "'")

Debug.Print "Postcodes: " & Postcode1 & ", " & Postcode2 & " Distance: " & GetDistanceKilometres(lat1, lon1, lat2, lon2) & " km"

End Function

Example Results (from the Immediate window):

?TestDistanceKilometres ("BS25 5NB", "TA23 0RP")
Postcodes: BS25 5NB, TA23 0RP Distance: 46.93 km

?TestDistanceKilometres ("SE1 7PB", "HA3 0SN")
Postcodes: SE1 7PB, HA3 0SN Distance: 15.072 km

?TestDistanceKilometres ("SE1 7PB", "BS7 8HP")
Postcodes: SE1 7PB, BS7 8HP Distance: 171.52 km

?TestDistanceKilometres ("SE1 7PB", "TA23 0RP")
Postcodes: SE1 7PB, TA23 0RP Distance: 230.867 km

Related Reading

Four of the most commonly used trigonometric functions are built in to the standard Access VBA reference library: Atn / Cos / Sin / Tan.

However, sometimes additional 'trig' functions are required. For example, drawing a circle on a map using VBA requires 2 additional trig functions ASin / Atn2.

My article Missing Trigonometric Functions includes code for 6 additional trig functions (ASin / ACos / ACot / ASec / ACsc / Atn2) not provided with Access together with the code needed to draw map circles.



Feedback

Please use the contact form below to let me know whether you found this article interesting/useful or if you have any questions/comments.

Please also consider making a donation towards the costs of maintaining this website. Thank you



Colin Riddington           Mendip Data Systems                 Last Updated 1 Jan 2024

Return to Code Samples Page

Return to Top